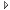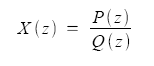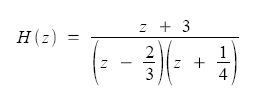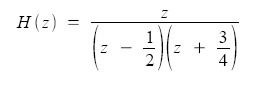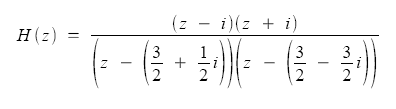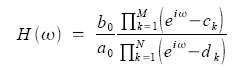| Tutorial 2 - Introduction to poles, zeros and the frequency response function |
|
This tutorial discusses pole-zero analysis of digital filters. Every digital filter can be specified by its poles and zeros (plus a gain factor). Poles and zeros give useful insights into a filter's response, and can be used as the basis for digital filter design. Since it is quite difficult to qualitatively analyse the Laplace transform and Z-transform of a system, as mappings of their magnitude and phase or real part and imaginary part result in multiple mappings of 2-dimensional surfaces in 3-dimensional space so we commonly examine plots of a transfer function's poles and zeros to try to gain a qualitative idea of what a system does. Once the Z-transform of a system has been determined, we can use the information contained in the polynomials to plot the function and more easily observe its defining characteristics. The Z-transform may be defined as:
The two polynomials, P (z) and Q(z), allow us to find the poles and zeros of the Z-Transform.
Definition 1: zeros 1. The value(s) for z where P (z) = 0. 2. The complex frequencies that make the overall gain of the filter transfer function zero. Definition 2: poles 1. The value(s) for z where Q(z) = 0. 2. The complex frequencies that make the overall gain of the filter transfer function infinite.
Example 1: Below is a simple transfer function:
Find the poles and zeroes of this function.
2. The Z-plane Once the poles and zeroes have been found for a given Z-transform, they can be plotted onto the Z-plane. The Z-plane is a complex plane with an imaginary and real axis referring to the complex-valued variable, z. The position on the complex plane is given by reiω and the angle from the positive, real axis around the plane is denoted by ω. When mapping poles and zeroes onto the plane, poles are denoted by an “x” and zeroes by an “o”. The figure below shows the Z-plane and zeroes onto the plane. 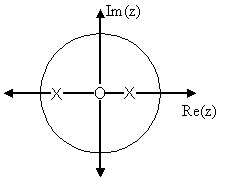
Figure 2. The circle represents the unit circle. Poles and zeroes plotted onto the complex plane for the transfer function:
Example 2: Plot the poles and zeroes of the transfer function given in Example 1 onto the complex plane.
Example 3: The poles and zeroes of a complex transfer function are somewhat more difficult to solve. Find the poles and zeroes of the following complex transfer functions, and plot them on the Z-plane. Remember: complex solutions will plot along the imaginary axis.
3. Frequency response and the Z-plane The frequency response may be written in terms of the system poles and zeros by substituting iω for z directly into the factored form of the transfer function. Based on the location of the poles and zeroes, we can quickly determine the frequency response. This is a result of the correspondence between the frequency response and the transfer function evaluated on the unit circle in the pole/zero plots. The frequency response of the system is defined as: 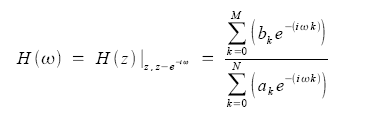
factoring the transfer function into poles and zeroes and multiplying both the numerator and denominator by eiω gives: |
|||||||||||
(i) | Find the poles and zeroes of the following transfer function: |
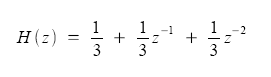
| (ii) | Plot the poles and zeroes of the function on the Z-plane |
| (iii) | Find the frequency response |
(iv) | Plot the filter characteristics H(ω) between 0 and 2π |
| (v) | What does this tell you about how the signal is being altered by the system? |
| < Prev | Next > |
|---|
In the Gallery: